intro to cryptography
Last meeting we learned about classical cryptography!
There were four challenges, which can be accessed under the Classical Cryptography set here:
Challenge 1
We have a Caesar Cipher with the ciphertext qvamzbaitilxcvpmzm. The ROT13 command in CyberChef can do a Caesar Cipher encryption/decryption for us, and we can check every key until we get some recognizable text. A shift of 18 does the trick, giving the plaintext insertsaladpunhere.
Challenge 2
A Vigenere ciphertext is given:
llgpzoxlwvgwzxacjmuudmmfghqzvvvpqtvceotjhlcvvbbaliznsgnqariujmkgwwqzzvmcjaqpvvvywwcltqifwvuvraxbgrvbvtxrlitmfntiwcyiilbrwqrffglyxstgfnimdccfgptzwxkwjcuqlmvokqhl
as well as a crib of vigenere. Because of properties of subtraction, if we decrypt the right part of the ciphertext with the crib, we’ll see a portion of the key. At an offset of 3 letters from the start, the decryption of the ciphertext with the crib is uritysec, which suggests that the key is security. This indeed decrypts the ciphertext into English.
Challenge 3
A long Vigenere ciphertext is given:
oclnrnwotlbqlpyexbvptqgygtxbanihatpenhauhoypuljfwhmcfllnqodmbbzvxrfcmsebllapnqlhmclviyxilvvbvluscofkbbqddybchsfoklgowhvtnsszniwuelxvwyhijaatxwlowhnuaymccfruuzevthdpneumyluoayhdksuhvgwpolksopuvlohgrfdhhoauldxbllydwjwyxilvvbvluscofktvwzdccissmmjldlumauusjlvtnraunssugicgfvuokpwujhavowuhqpjgkbqtgyvovselbbaujlngkkjguvudmsylosjhwebpwjbiklllupwtfslpqgjuaymbgawhjhqvvfwholhojlhcaujtxifkffkadnmhzptwktblrtwupkelhtrbydpawudnmbgaxokalnpaqwssuprubhatfcfslnnwzhwslvpoesgugfgtvulvkpnddlwhrbyzbbviuawqzvvhqvxwxidkohmugeaglhorwchrhcfl
The first step is to find the most likely key length. We’ll use the python3 interpreter on tio.run for this. The ciphertext can go into the input field and we can retrieve it with a call to input(). We’ll also want a way to calculate index of coincidence, which we can code up according to the formula listed on Wikipdia.
from collections import Counter
ct = input()
def ic(message):
N = len(message)
return 26 * sum(freq*(freq-1) for letter, freq in Counter(message).items())/(N * (N-1))
Now for each key length n, we’ll want to find the average index of coincidence across all messages constructed by taking every nth character from the original message, which ensures that each of the smaller messages is encrypted by the same key byte. Code below:
for keylen in range(1,31):
sum_ic = 0
for offset in range(keylen):
sum_ic += ic(ct[offset::keylen])
avg_ic = sum_ic/keylen
print(keylen, avg_ic, sep='\t')
Here’s the output of this code:
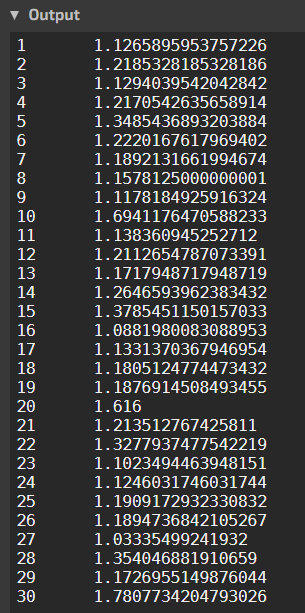The index of coincidence of English is about 1.73, and we can see that a key length of 10 comes pretty close, at 1.69. So, we can be pretty sure that the length of the key is 10.
Now, for actually finding the key, we’ll pick key letters that make the frequency distribution of the letters they encode as close as possible to the frequency distribution of English letters, which we’ll rip off of Wikipdia. We’ll take “close” to mean the least sum of squared differences between frequencies. Code below:
from string import ascii_lowercase as alphabet
freq_english = {"a":8.2,"b":1.5,"c":2.7,"d":4.7,"e":13,"f":2.2,"g":2,"h":6.2,"i":6.9,"j":0.16,"k":0.81,"l":4.0,"m":2.7,"n":6.7,"o":7.8,"p":1.9,"q":0.11,"r":5.9,"s":6.2,"t":9.6,"u":2.7,"v":0.97,"w":2.4,"x":0.15,"y":2,"z":0.078}
keylen = 10
for offset in range(keylen):
c = ct[offset::keylen]
best = -1
leastsquares = float('inf')
for shift in range(26):
f = {alphabet[(alphabet.find(i)-shift+26)%26]: c.count(i)/len(c) for i in alphabet}
sumsquares = sum((f[i]-freq_english[i])**2 for i in alphabet)
if sumsquares < leastsquares:
leastsquares = sumsquares
best = shift
print(alphabet[best],end='')
This gives the output boshdajosh, which seems like it should be the key since it produces a decryption of
notgonnabeactiveondiscordtonightimmeetingagirlarealoneinhalfanhourwouldntexpectalotofyoutounderstandanywaysopleasedontdmmeaskingmewhereiamimwiththegirlokyoullmostlikelygetairedbecauseillbewiththegirlagainidontexpectyoutounderstandshesactuallyreallyinterestedinmeanditsnotasituationicanpassupforsomemeaninglessdiscorddegeneratesbecauseillbemeetingagirlnotthatyoureallyaregoingtounderstandthisismylifenowmeetingwomenandnotwastingmyprecioustimeonlineihavetomoveonfromsuchsimplethingsandbranchoutyouwouldntunderstandeveryone
and indeed that is our answer.
By the way, there are websites (namely this one) that can do this all for you.
Challenge 4
This challenge goes similarly to the previous one. The exact same code for index of coincidence still works, and yields a key length of 29. However, in this case we can use a bit of a shortcut for finding the key bytes. By far the most common character in English text is the space character, so we can just pick key bytes that maximize the number of spaces in the output. Code below:
keylen = 29
key = []
for i in range(keylen):
c = ct[i::keylen]
key.append(max(range(256),key=lambda x: c.count(ord(' ')^x)))
Once you get the key, you can either decode the message in CyberChef, or write a quick XOR implementation in python.
decrypted = []
for i in range(len(ct)):
decrypted.append(ct[i] ^ key[i % len(key)])
print(bytes(decrypted))
This gives us the flag: UMDCTF{d1d_y0u_use_k4s!sk1_0r_IoC???}